Modern Computer Architecture and Organization
Modern Computer Architecture and Organization, by Jim Ledin. Published by Packt Publishing.
Chapter 6, Exercise 2
A common form of the one-dimensional discrete cosine transform is:
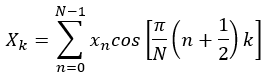
In this formula, k, the index of the DCT coefficient, runs from 0 to N-1.
Write a program to compute the DCT of the sequence x={0.5,0.2,0.7,-0.6,0.4-0.2,1.0,-0.3}.
Note that the cosine terms in the formula depend only on the indexes n and k, and do not depend on the input data sequence x. This means the cosine terms can be computed one time and stored as constants for later use. Using this approachas a preparatory step, the computation of each DCT coefficient reduces to a sequence of MAC operations.
Note also that this formula represents the un-optimized form of the DCT computation, requiring N2 iterations of the MAC operation to compute all N DCT coefficients.
Answer
See the python file Ex__2_dct_formula.py for the DCT code.
To run the code, assuming python is installed and is in your path, execute the command python Ex__2_dct_formula.py
This is the output produced by the program:
C:\>Ex__2_dct_formula.py
Index 0 1 2 3 4 5 6 7
x 0.5000 0.2000 0.7000 -0.6000 0.4000 -0.2000 1.0000 -0.3000
DCT(x) 1.7000 0.4244 0.6374 0.4941 -1.2021 0.5732 -0.4936 2.3296